In un precedente articolo abbiamo parlato degli indici di tendenza centrale (media, moda e mediana). Questa volta analizzeremo gli indici di variabilità. In particolar modo concentreremo la nostra attenzione sulla deviazione standard, sulla varianza e sul coefficiente di variazione e la loro implementazione in SPSS, in R studio e in Excel.

Cosa sono gli indici di dispersione (o indici di variabilità)
In generale, gli indici di dispersione ci dicono quanto i valori si disperdono intorno alle misure di tendenza centrale, ovvero quanto si disperdono intorno al valore più rappresentativo del centro della distribuzione: più l’indice di variabilità è grande, maggiore sarà la variabilità dei dati che sto analizzando.
Utilizziamo gli indici di dispersione quando la variabile considerata è di tipo quantitativo o se è misurata su scala a intervalli o a rapporti equivalenti.
Come calcolare la Varianza e la varianza campionaria corretta
Un modo per calcolare la variabilità dei dati tenendo conto di tutti i valori della distribuzione, consiste nel calcolare la distanza (o scarto) di ciascun valore dalla media.
Se sommiamo i quadrati delle deviazioni o scarti dalla media e dividiamo questa somma per il numero delle osservazioni otteniamo la varianza.
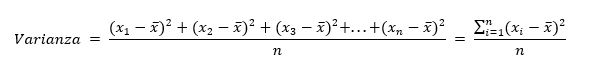
ESEMPIO:
Nel seguente esempio viene analizzata la varianza della variabile età.

Facciamo, come prima cosa, la media delle osservazioni.
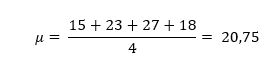
Ora possiamo utilizzare la media ottenuta per il calcolo della varianza.
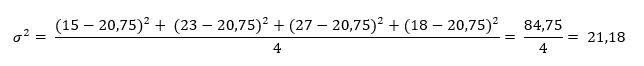
Quando la varianza viene calcolata su una popolazione, si indica con il simbolo greco σ2 ; quando, invece, viene calcolata su un campione si indica con s2. Nel caso in cui la varianza viene calcolata su un campione, inoltre, il denominatore n è sostituito da n-1 così da ottenere una stima corretta della dispersione della variabile nella popolazione da cui il campione in esame è stato estratto: si parla, infatti, di varianza campionaria corretta.
Un limite della varianza come misura di dispersione è quella di avere una unità di misura espressa al quadrato. Per questo motivo, si ricorre, molto spesso, al calcolo della deviazione standard.
Deviazione standard: cos’è e come calcolarla
La deviazione standard, in generale, è pari alla radice quadrata della varianza.
A differenza di quest’ultima, la deviazione standard è un indice che viene espresso con la stessa unità di misura dei valori osservati. Indica quanto, in media, ciascun valore si discosta dalla media della popolazione.
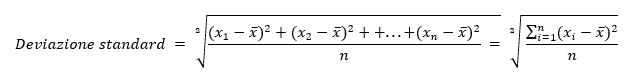
ESEMPIO:
Considerando l’esempio precedente, applichiamo solamente il radicando.
![]()
Questo indice di dispersione può essere interpretato anche come misura di accuratezza della media: più la deviazione standard è elevata, meno la media è efficace nel fornire un valore che sia rappresentativo dell’intera distribuzione.
Anche in questo caso, se la deviazione standard viene calcolata sulla popolazione intera, si usa la lettera greca σ ; invece, se viene calcolata su un campione si utilizza la lettera s (o ds).
Un limite della deviazione standard è rappresentato dal fatto che non è un indice adatto per confrontare la dispersione di distribuzioni i cui punteggi sono espressi in unità di misura differenti.
Una misura di dispersione che non risente dell’unità di misura è il coefficiente di variazione.
Coefficiente di variazione: cos’è e quando si usa
Il coefficiente di variazione è un indice che si basa sul rapporto tra deviazione standard e media:
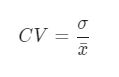
Attenzione: da non confondere con l’intervallo di variazione!
Questo indice esprime il grado di dispersione dei punteggi in termini di scostamento percentuale dalla media. Viene chiamato anche deviazione standard relativa.
È utile quando si vuole confrontare la dispersione di distribuzioni i cui punteggi sono espressi da unità di misure differenti.
ESEMPIO:
Consideriamo ora, oltre ai dati usati in precedenza, la media dei voti di 4 studenti e la relativa deviazione standard.
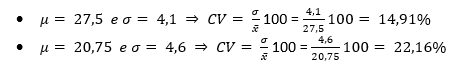
Si legge come: “in media i punteggi si discostano dal valore centrale di una quantità pari a circa il 22% della media”.
In questo esempio specifico, notiamo che il coefficiente di variazione della seconda distribuzione (distribuzione espressa in anni) ha una dispersione maggiore rispetto alla prima distribuzione (espressa in voti).

Varianza, deviazione standard e coefficiente di variazione in excel
- Riportiamo su un foglio Excel i dati di esempio:
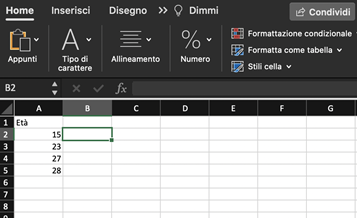
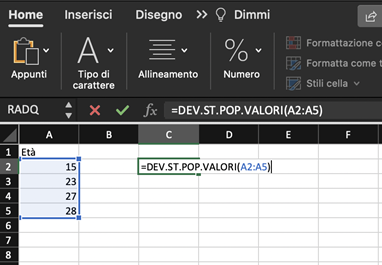
- Su una qualunque cella vuota scriviamo il comando “VARIANZA.POP.VALORI” preceduto dall’uguale; nelle parentesi vanno inseriti i dati per il calcolo della varianza; premere invio.
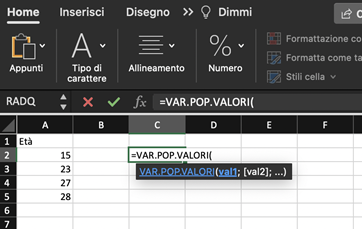
Si procede in modo analogo per il calcolo della deviazione standard.
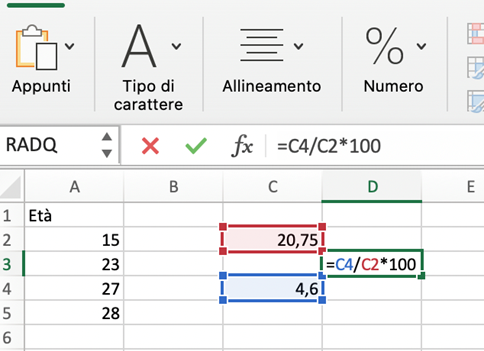
Il coefficiente di variazione non ha una formula propria. Per questo dovremmo calcolarlo a “mano”: ci posizioniamo in una cella vuota di Excel; digitiamo l’uguale; selezioniamo la cella della deviazione standard; digitiamo l’operatore di divisione; selezioniamo la cella della media; moltiplichiamo il tutto per 100.
Varianza, deviazione standard e coefficiente di variazione in R Studio
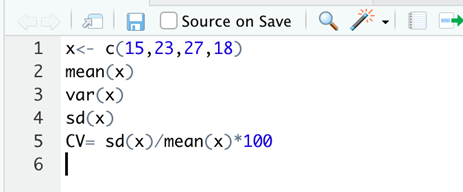
Per calcolare gli indici In R Studio, bisognerà creare un vettorecon i valori età “x” e usare il comando mean() per la media, var() per la varianza e sd() per la deviazione standard. Per il coefficiente di variazione non esiste un comando specifico: quindi utilizzeremo i comandi precedenti per la formula del coefficiente di variazione andando a dividere sd() e mean() e infine moltiplicandolo per 100.
Varianza, deviazione standard e coefficiente di variazione in SPSS
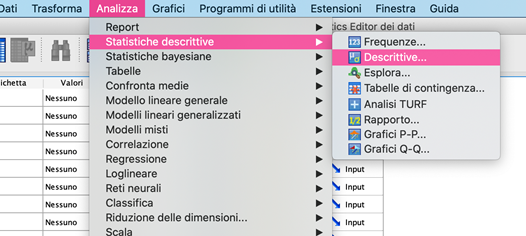
- Per calcolare gli indici di varianza e deviazione standard in SPSS, dal menù Analizza, selezionare Statistiche descrittive e poi frequenza.
- A questo punto si aprirà una finestra di dialogo: selezionare la variabile (quantitative) per cui calcoleremo i due indici. Selezionare l’opzione Statistiche.
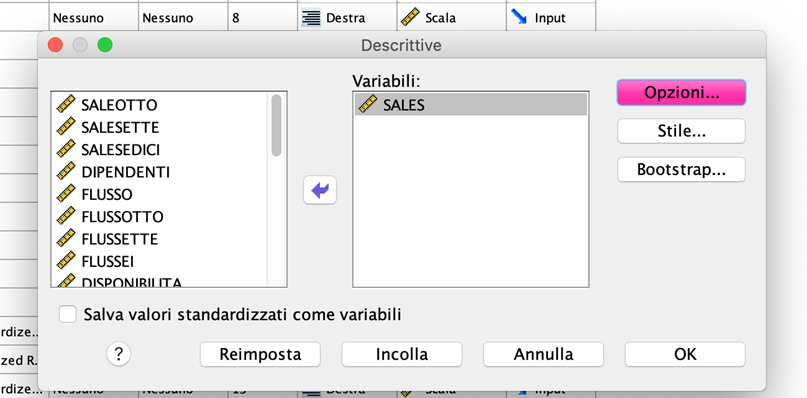
- Flaggare Varianza e deviazione standard dall’elenco di statistiche proposte. Diamo Continua e Ok per confermare le nostre scelte e visualizzare i risultati.
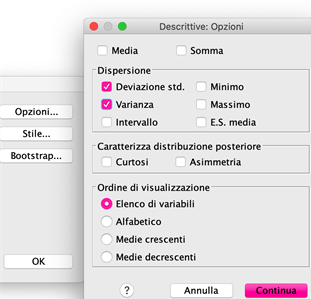
Per il calcolo del coefficiente di variazione, invece, anche in SPSS non esiste una formula specifica o un’opzione da “flaggare”. Si ricorre a questo punto al classico calcolo “a mano”: dalla finestra di dialogo introdotta in precedenza, si seleziona, oltre alla deviazione standard, anche la media. Diamo il “continua” e l’ok per visualizzare i risultati. A questo punto prendiamo il valore della deviazione standard e lo dividiamo per la media della distribuzione; infine moltiplichiamo per 100.
Hai ancora dubbi sul calcolo degli indici di variabilità o hai bisogno di una nostra consulenza per un problema specifico?
Nessun problema, scrivici e spiegaci la tua necessità! Il preventivo è gratuito e senza impegno!

Articolo a cura della Dott.ssa Aurelia Colucci





