MEDIA MODA E MEDIANA: a che cosa servono e come calcolarle?

Gli indici di centralità (media, moda e mediana) sono lo strumento di sintesi per eccellenza, in grado di riassumere le informazioni di una variabile rilevata ad esempio tramite un’indagine statistica.

Ma perché sono così largamente utilizzate?

Tutto nasce dal bisogno di ottenere un indice che ci permetta di descrivere, nel modo più semplice possibile, un fenomeno misurabile come altezza, peso, reddito medio annuo, ma anche titolo di studio o religione professata.

Faremo un semplice esempio pratico, che ci permetta di capire meglio la definizione di ogni indice e le differenze tra loro. Supponiamo di avere una classe di 10 studenti, di cui riportiamo il voto ottenuto all’esame di Statistica

Iniziamo introducendo alcuni concetti che saranno utili in seguito:

• l’insieme delle unità oggetto di studio saranno la nostra popolazione di riferimento, in questo caso gli studenti
• il voto sarà la nostra variabile d’interesse e la sua distribuzione è costituita dall’insieme di tutti i valori osservati (chiamati anche “termini” della distribuzione) di tale variabile, ovvero, i singoli voti.

La media aritmetica è forse lo strumento statistico più conosciuto ed utilizzato, tanto da diventare l’emblema della Statistica stessa.

Può essere calcolata per variabili quantitative ed è definita come:

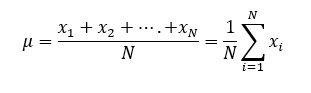
ovvero la media aritmetica di una distribuzione è la somma dei termini  divisa per il numero di osservazioni N.

Volendo quindi calcolare la media dei voti dei nostri studenti, sarà:

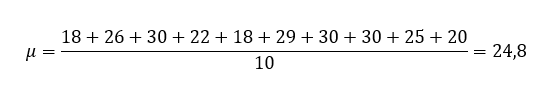
La media aritmetica è però un indice poco robusto, ovvero è fortemente influenzata dai termini della distribuzione, soprattutto da quei termini che si discostano molto dagli altri, chiamati outliers.

Facciamo un esempio, andiamo a sostituire un qualunque valore della precedente distribuzione, con uno molto distante numericamente dagli altri:

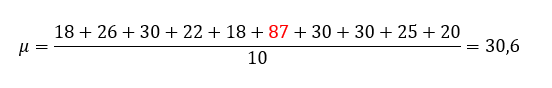
Come possiamo notare, il risultato ottenuto è sensibilmente diverso rispetto al precedente. Tralasciando il fatto che è ovviamente impossibile avere un voto pari a 87, errori nella trascrizione dei dati non sono rari e la media aritmetica ne potrebbe risentire.

Un indice molto più robusto è la mediana, che viene calcolata in maniera differente rispetto alla media aritmetica, in quanto è necessario ordinare in modo crescente i termini della distribuzione e può essere calcolata per variabili quantitative di tipo continuo e ordinale.

Una volta quindi ottenuta la distribuzione ordinata ,, la mediana è:

• per N dispari la quantità  , ovvero il termine che occupa il posto centrale della distribuzione
• per N pari la quantità , ovvero la media aritmetica dei termini centrali 

Volendo quindi calcolare la mediana dei voti in Statistica, dovremo considerare i termini che occupano il posto 5 e 6 e farne la media aritmetica

ovvero m=25,5.

Se in questo caso, sostituissimo un valore con un outlier, il risultato non cambierebbe

La mediana può essere calcolata per tutte le variabili quantitative ed anche per le variabili qualitative ordinali (come ad esempio per il titolo di studio).

La moda, a differenza della media aritmetica e della mediana, può essere calcolata per qualsiasi tipo di variabile.

Per la spiegazione della moda, introduciamo un ulteriore concetto, ovvero la distribuzione di frequenze. Per distribuzione di frequenze, intendiamo uno schema in cui si riassume quante volte un termine della distribuzione si presenta nella popolazione d’interesse:

La moda, quindi, non è altro che il termine della distribuzione che presenta la frequenza più alta, nel nostro caso il voto 30.

È inoltre l’unico indice che può essere calcolato anche per le variabili qualitative non ordinabili (come, ad esempio, il colore degli occhi o la religione professata).

Vediamo ora come calcolare media aritmetica, mediana e moda su Excel, R e SPSS.

Media, moda e mediana in Excel

1. Riportiamo su un foglio Excel i dati di esempio:
2. Una qualunque cella vuota scriviamo il comando “MEDIA”, preceduto dall’uguale; all’interno della parentesi va indicata l’area del foglio in cui sono contenuti i dati, aiutandosi con le coordinate (“lettere” per indicare le colonne, “numeri” per indicare le righe); premere invio
3. Su una qualunque cella vuota scriviamo il comando “MEDIANA”, preceduto dall’uguale; all’interno della parentesi va indicata l’area del foglio in cui sono contenuti i dati, aiutandosi con le coordinate (“lettere” per indicare le colonne, “numeri” per indicare le righe); premere invio
4. Su una qualunque cella vuota scriviamo il comando “MODA.MULT”, preceduto dall’uguale; all’interno della parentesi va indicata l’area del foglio in cui sono contenuti i dati, aiutandosi con le coordinate (“lettere” per indicare le colonne, “numeri” per indicare le righe); premere invio

Media, moda e mediana in R

Per calcolare i tre indici su R, basterà creare un vettore con i valori dei voti “x” e usare il comando mean() per calcolare la media, il comando median() per la mediana e il comando table(), che fornirà in output la distribuzione di frequenze.

Media, moda e mediana in SPSS

1. Per calcolare gli indici in SPSS, dal menù Analizza, selezionare Statistiche descrittive e poi Frequenze.
2. Si aprirà una finestra di dialogo: nella sezione Variabili, andremo ad inserire la variabile per la quale vogliamo calcolare i nostri indici. Selezioniamo ora l’opzione Statistiche
3. Troveremo un elenco di statistiche che è possibile calcolare e tra queste selezioniamo media, mediana e moda, tra gli indici di tendenza centrale. Diamo Continua e Ok per confermare le nostre scelte ed otterremo i nostri risultati

Se hai ancora dei dubbi e vuoi una consulenza su questo argomento, così come su tanti altri, non esitare a contattarci!