In questo articolo parleremo dei test statistici (detti anche t-test o test di verifica d’ipotesi).
Dopo aver dato una definizione generale faremo un breve focus su cos’è il p-value, per poi andare ad analizzare i vari tipi di t-test.
Infine, vedremo come i test statistici possono essere effettuati tramite SPSS, R e Excel.
Se vuoi approfondire la conoscenza di questo e altri argomenti statistici contattaci.

Cosa sono i test statistici
I test statistici sono una procedura che ci permette di determinare se il campione di dati osservati conferma o nega un’ipotesi, cioè se (e con quale grado di certezza) sia possibile estendere alla popolazione una data evidenza presente nel nostro campione.
I test mettono a confronto due ipotesi:
- H0, chiamata “ipotesi nulla“,
- H1, chiamata “ipotesi alternativa“
L’ipotesi nulla è presunta vera (es: tutti i corvi sono neri) e attraverso i dati raccolti cerchiamo prove per rifiutare l’ipotesi nulla accettando così l’ipotesi alternativa (in altre parole: per dimostrare che H0 è falsa è necessario trovare un corvo NON nero).
La base di ogni test statistico è un calcolo che viene effettuato sui dati campionari raccolti e che cambia a seconda del tipo di test: prende il nome di ‘Statistica Test’ (nel nostro caso si tratta della statistica test t di Student).
Alcune statistiche test presentano i gradi di libertà, che servono a identificare la curva e che dipendono dal tipo di test.
Quello di cui siamo a conoscenza è la distribuzione dei valori delle statistiche del test quando l’ipotesi nulla è vera:
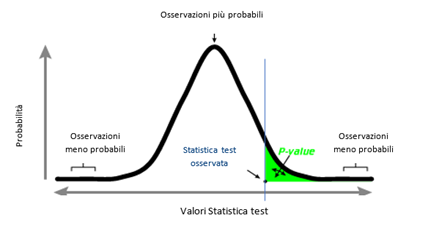
Che cosa è il p-value?
Il p-value rappresenta (tecnicamente) la probabilità di ottenere valori delle statistiche del test uguali o maggiori di quello osservato (in valore assoluto).
In altre parole, è la probabilità di sbagliare rifiutando l’ipotesi nulla, cioè la probabilità di scegliere erroneamente H1 poiché H0 è vera nella popolazione (c’è sempre una probabilità di sbagliare rifiutando H0 con i dati raccolti).
Avremo quindi che, più piccolo è il p-value, maggiori saranno le probabilità di rifiutare in sicurezza l’ipotesi nulla, perché sapremo che così facendo la probabilità di commettere errori è bassa.
Essendo una probabilità, varia tra 0 escluso e 1 incluso.
Pertanto, un p-value grande indica che i dati sono compatibili con l’ipotesi nulla, mentre un p-value piccolo indica che possiamo rifiutare H0 e accettare ragionevolmente H1.
Quanto deve essere piccolo il p-value? In letteratura ci sono dei livelli riconosciuti chiamati α, cioè delle soglie convenzionali al di sotto delle quali l’ipotesi nulla può essere rifiutata: la più usata è 0,05.
Quali sono le tipologie di t-test e a cosa servono
Esistono tre tipologie principali di t-test, ovvero il t-test a campioni singolo, il t-test a campioni appaiati (o accoppati) e il t-test a campioni indipendenti. In base al tipo di ipotesi da verificare sceglieremo il t-test più adatto allo scopo.
T-test a campione singolo
Il t-test a campione singolo si utilizza quando vogliamo determinare se i dati del campione ci consentono di concludere che il valore medio di una variabile numerica può o meno essere uguale a un certo valore nella popolazione.
In questo caso avremo due ipotesi:
- H0: µ = valore definito dall’utente (x)
- H1: µ ≠ valore definite dall’utente (x)
Questo test è basato sulla seguente statistica test:

dove s rappresenta la deviazione standard del campione e n la numerosità campionaria.
La statistica test ottenuta viene confrontata con le tabelle della distribuzione t di Student con (n-1) gradi di libertà.
Il p-value è ottenuto nelle tabelle (o fornito dal software) ed è la probabilità di sbagliare rifiutando l’ipotesi nulla.
Quindi prenderemo una decisione in base al valore del p-value.
T-test a campioni appaiati
Il t-test a campioni appaiati (o accoppiati) viene utilizzato quando abbiamo due variabili numeriche misurate sugli stessi individui (ad esempio, il peso di un gruppo di persone prima e dopo una certa dieta).
Serve per verificare l’uguaglianza delle medie delle due variabili.
Le ipotesi saranno quindi:
- H0: µ1 = µ2
- H1: µ1 ≠ µ2
Oppure, se chiamiamo “d” la differenza: d = (µ 1 – µ 2):
- H0: d = 0
- H1: d ≠ 0
Questo test è basato sulla seguente statistica test:
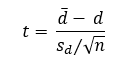
dove sd rappresenta la deviazione standard della variabile ottenuta come differenza tra le due variabili originali a confronto, d la media di questa nuova variabile e n la numerosità campionaria.
Anche in questo caso la statistica test ottenuta viene confrontata con le tabelle della distribuzione t di Student con (n-1) gradi di libertà.
Questa volta accettare H0 significa che la differenza tra i due gruppi non è significativamente diversa da zero, mentre rifiutare H0 significa affermare che c’è una differenza significativa nelle medie.
T-test a campioni indipendenti
Il t-test a campioni indipendenti si utilizza quando vogliamo determinare se i dati del campione ci consentono di concludere che il valore medio di una variabile numerica in due sottogruppi indipendenti (cioè, contenente soggetti diversi) è significativamente diverso (es: età media tra maschi e femmine).
Le ipotesi saranno:
- H0: µ1 = µ2
- H1: µ1 ≠ µ2
E così, possiamo anche riscrivere in termini di differenza:
- H0: µ1 – µ2 = 0
- H1: µ1 – µ2 ≠ 0
Questo test è basato sulla seguente statistica test:
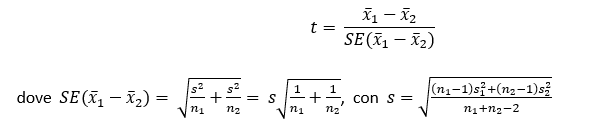
La statistica test ottenuta viene confrontata con le tabelle della distribuzione t di Student con (n-2 = n1+n2-2) gradi di libertà.
Il t-test a campioni indipendenti, però, necessita di una condizione da verificare per poter essere sicuri che dia dei risultati affidabili: l’uguaglianza (omogeneità) delle varianze della variabile contenente i due sottogruppi.
Per verificare questa condizione si utilizza il test di Levene.
Test di Levene
Prima di effettuare il t-test a campioni indipendenti è, quindi, necessario verificare che la varianza della variabile numerica non sia significativamente diversa nei due sottogruppi.
Usiamo l’F-test chiamato test di Levene.
Le ipotesi sono:
- H0: s21 = s22
- H1: s21 ≠ s22
Cosa succede se il test di Levene rifiuta l’ipotesi nulla di varianze omogenee?
Possiamo comunque fare il test, ma dovremo usare una particolare versione del t-test assumendo varianze disuguali.

T-test su Excel
Come svolgere i test statistici su Excel? Per svolgere questi test utilizziamo il componente aggiuntivo “Strumenti di analisi” presente su Excel.
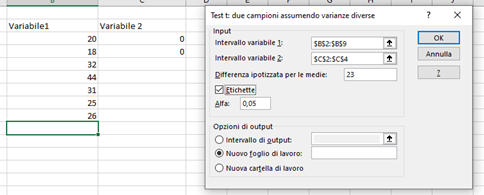
Per quanto riguarda il t-test a campione singolo creiamo due colonne: quella di interesse e una contenente due valori pari a zero; da “Dati” ➜ “Analisi dati” selezioniamo “Test t: due campioni assumendo varianze diverse”:
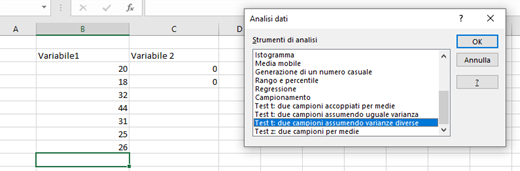
A questo punto selezioniamo le colonne nei due intervalli della finestra grafica che appare, scriviamo il valore di x che ipotizziamo (es: 23), mettiamo la spunta a “etichette” (se selezionando le colonne abbiamo compreso il nome delle variabili), e settiamo il valore di α (di default è 0,05).
Non resta che cliccare su OK: avremo una tabella con i risultati.
Nota: bisogna cancellare la colonna della variabile 2 nella tabella e dare il nome giusto al test, dato che la funzione esatta per il t-test a campione singolo non c’è).
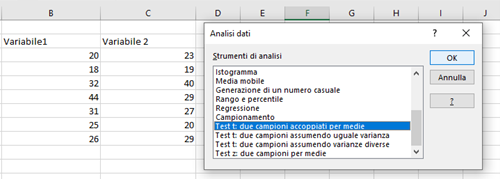
Per il t-test a campioni accoppiati creiamo due colonne contenenti le variabili di interesse e utilizziamo lo stesso strumento di analisi precedente, in cui questa volta selezioniamo “Test t: due campioni accoppiati per medie”.
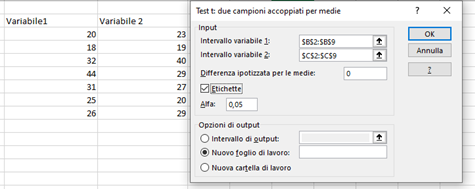
Come prima, selezioniamo le colonne nei due intervalli della finestra grafica che appare, scriviamo il valore della differenza, ovvero 0, mettiamo la spunta a “etichette” (se selezionando le colonne abbiamo compreso il nome delle variabili), e settiamo il valore di α (di default è 0,05).
Non resta che cliccare su OK: avremo una tabella con i risultati.
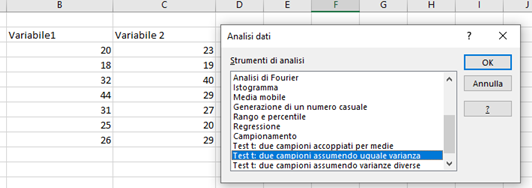
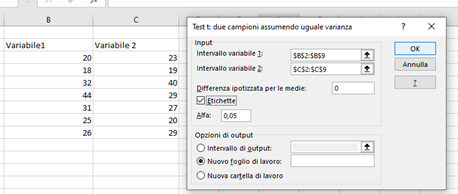
Per il t-test a campioni indipendenti creiamo due colonne contenenti le variabili di interesse e utilizziamo lo stesso strumento di analisi precedente, in cui questa volta selezioniamo “Test t: due campioni assumendo uguale varianza”, se abbiamo accettato l’ipotesi di omogeneità delle varianze, o “Test t: due campioni assumendo varianze diverse” se abbiamo rifiutato l’ipotesi di omogeneità delle varianze.
Come prima, selezioniamo le colonne nei due intervalli della finestra grafica che appare, scriviamo il valore della differenza, ovvero 0, mettiamo la spunta a “etichette” (se selezionando le colonne abbiamo compreso il nome delle variabili), e settiamo il valore di α (di default è 0,05).
Non resta che cliccare su OK: avremo una tabella con i risultati.
Se hai ancora dubbi non esitare a contattarci cliccando QUI!
T-test su SPSS
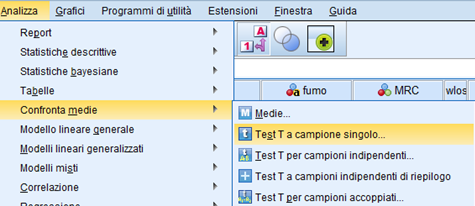
Per quanto riguarda SPSS andiamo su Analizza ➜ Confronta medie ➜ t test di interesse
Per il t-test a campione singolo scegliamo, appunto, “T test a campione singolo”:
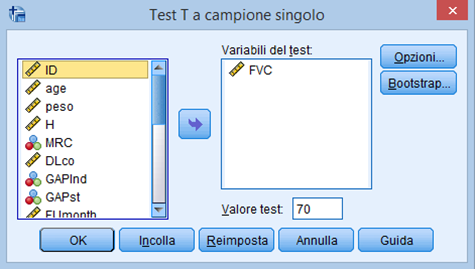
Nella finestra che ci si apre selezioniamo la variabile numerica su cui condurre il test e inseriamo il valore della media da testare:
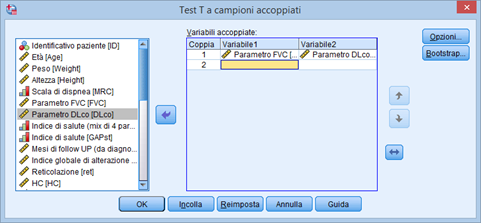
Per il t-test a campioni appaiati scegliamo, appunto, “T test per campioni accoppiati”:
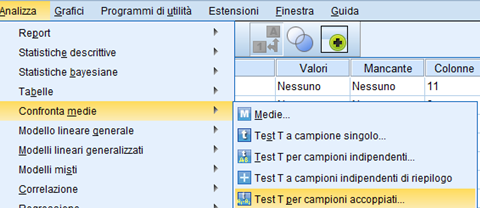
Nella finestra che ci si apre selezioniamo le due variabili numeriche su cui condurre il test.
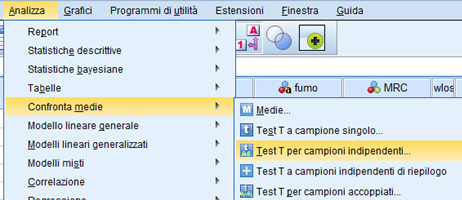
Per il t-test a campioni indipendenti scegliamo, appunto, “T test per campioni indipendenti”:
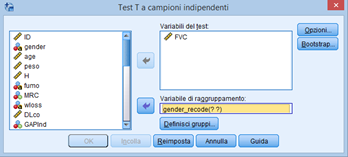
Nella finestra che ci si apre selezioniamo la variabile numerica su cui condurre il test e la variabile relativa ai due gruppi, da definire (dipende da come li abbiamo codificati):
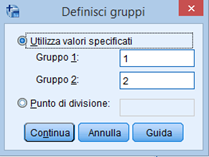
Il test di Levene per l’omogeneità delle varianze comparirà nell’output insieme ai risultati del t-test.
Vuoi imparare a utilizzare il software per le tue analisi? Chiedi informazioni sui nostri corsi, anche per principianti, cliccando QUI!
T-test su R
Per quanto riguarda il software R utilizziamo la funzione t.test() per tutte e tre le tipologie di analisi.
Relativamente al t-test a campione singolo passiamo alla funzione solo due argomenti: il nome della variabile numerica e il valore della media da testare:

Relativamente al t-test a campioni appaiati passiamo alla funzione il nome delle due variabili numeriche di interesse e scriviamo TRUE nell’argomento paired:
![]()
Relativamente al t-test a campioni indipendenti bisogna prima svolgere il test di Levene: carichiamo il pacchetto car e utilizziamo la funzione leveneTest, a cui passiamo come argomenti la variabile numerica di interesse e la variabile contenente i due gruppi:
![]()
A questo punto procediamo con il t-test a campioni indipendenti usando la funzione t.test, a cui passiamo come argomenti la variabile numerica e la variabile relativa ai due gruppi, separate dalla tilde, e nell’argomento var.eq scriviamo TRUE o FALSE in base al risultato del test di Levene:

Per qualsiasi chiarimento non esitare a contattarci!
Offriamo corsi per imparare l’utilizzo di Excel, SPSS ed R, con rilascio di un attestato di frequenza.

Articolo a cura della Dott.ssa Alessandra Cardinale





