La meta-analisi rappresenta la tecnica statistica maggiormente utile ed utilizzata per l’analisi della letteratura scientifica, permettendo di combinare i dati provenienti da studi diversi e fornendo così una visione più chiara e complessiva del fenomeno in esame. In questo articolo, esploreremo passo dopo passo come realizzare una meta-analisi partendo da zero, dalla definizione degli obiettivi alla scelta dei modelli statistici, offrendo un’approfondita guida per coloro che desiderano avventurarsi nell’analisi di studi esistenti per trarne conclusioni più robuste e generali.
Nel dettaglio vedremo:
Che cos’è la meta-analisi
Come scegliere gli articoli per una meta-analisi
Meta-analisi: diverse tipologie
Meta-analisi passo passo
Meta-analisi: SPSS, R o Stata?

Che cos’è la meta-analisi
La Meta-Analisi è una particolare tecnica utilizzata nella revisione sistematica della letteratura, in cui vengono valutati e combinati i risultati di diverse sperimentazioni, con bassa numerosità campionaria (es. patologie rare) o risultati discordanti (es. efficacia di un farmaco), relative a uno stesso argomento. Con questa tecnica possiamo arrivare a conclusioni più affidabili e con una maggior potenza statistica. È importante saper scegliere gli studi da considerare, in quanto bisogna conoscere e cercare di ridurre i bias (es: caratteristiche simili dei pazienti, stando attenti ai criteri di inclusione e di esclusione).
Per condurre l’analisi bisogna sapere come costruire un campione, a partire dalla sua numerosità: estrapoleremo le informazioni dai vari studi, in quanto non si hanno a disposizione i dataset originali di ogni paper. In questo caso le unità non saranno i singoli soggetti, ma gli studi coinvolti.
In casi come questo gli studi esistenti sono condotti su una numerosità ridotta, ma sono comunque da ritenere molto utili: combinando i diversi risultati ottenuti è possibile ottenere delle conclusioni più rilevanti, supportate da una più elevata potenza statistica!
L’obiettivo è, quindi, combinare i diversi risultati ottenuti negli studi a disposizione in letteratura e ottenere delle conclusioni più rilevanti supportate da una più elevata potenza statistica!
Come scegliere gli articoli per una meta-analisi
Quando decidiamo di condurre questo tipo di ricerca, la prima cosa da stabilire è il fenomeno che si vuole studiare. Una volta scelto l’oggetto di studio, bisogna ricercare gli articoli esistenti ed effettuare una scrematura, in modo da avere:
- compatibilità di metodologia (es: stessi criteri di inclusione ed esclusione);
- dati esatti (es: se alcuni risultati vengono riportati solo tramite grafici, potrebbe non essere possibile reperire il dato di interesse).
Un altro problema che bisogna porsi è: di quanti articoli abbiamo bisogno per condurre la meta-analisi? Per rispondere a questa domanda bisogna andare a calcolare la potenza della nostra meta-analisi, dovuta ai dati contenuti nei vari studi.
Una volta stabilito il fenomeno di studio, bisogna andare a fare la selezione degli articoli, che è una fase è molto importante. Generalmente i passi sono:
- Estrazione articoli da diverse riviste online;
- Eliminazione articoli duplicati;
- Esclusione di articoli per titolo e abstract;
- Aggiunta di articoli dalla bibliografia;
- Esclusione (a causa dell’argomento) articoli dopo lettura integrale del testo;
- Esclusione articoli per assenza di dati estrapolabili;
- Totale definitivo di articoli inclusi.
Se alla fine gli studi non dovessero essere molti, bisognerà specificarne le cause nell’articolo che si vuole produrre (si sconsiglia un numero minore di 3 generalmente).
Meta-analisi: le diverse tipologie
La meta-analisi può essere condotta sia su risultati continui, ad esempio la riduzione di eventi per una determinata patologia, che su risultati binari, come il numero di eventi in un gruppo (o due).
Per condurre questo tipo di analisi abbiamo bisogno di costruire un dataset in cui ogni riga è uno studio, mentre le colonne devono riportare:
- Numerosità del gruppo considerato
- Valore del risultato continuo (es. media e deviazione standard) o binario (es. numero eventi)
- Riferimento al paper (nome, id, stato, anno pubblicazione,…)
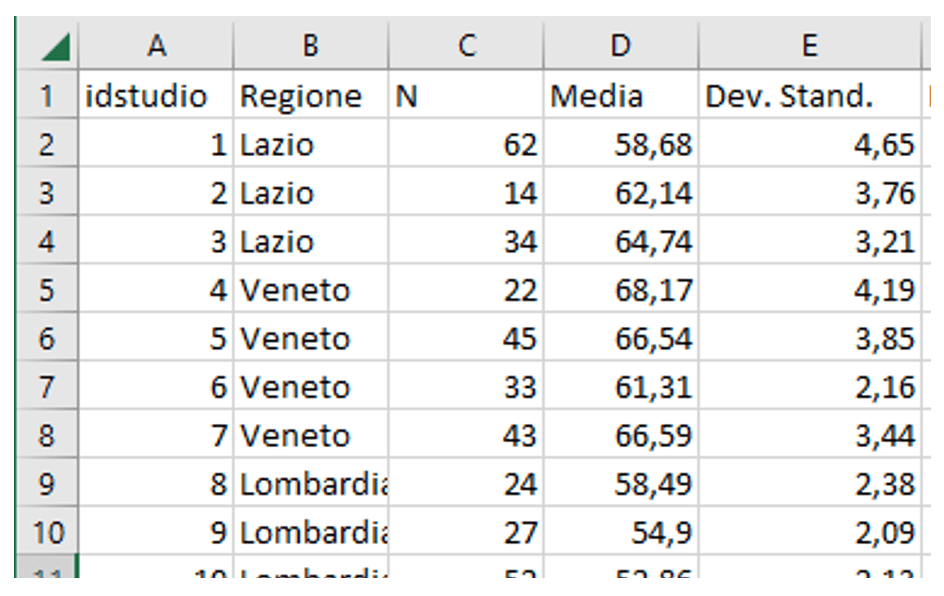
Se hai dubbi su come costruire il dataset contattaci!
Meta-analisi passo passo
Una volta che il dataset è pronto possiamo iniziare le analisi. Prima di arrivare alle conclusioni per capire se l’effetto globale sia significativo oppure no, bisogna fare diversi passaggi, il primo dei quali è capire che tipo di modello vada utilizzato: effetti fissi o random?
Eterogeneità: modello a effetti fissi o random?
Per capire quale sia il modello adatto al dataset a disposizione, dobbiamo per prima cosa andare a calcolare omogeneità e il relativo test: il test dell’omogeneità si basa sulla Q di Cochran, in cui si hanno due ipotesi:
H0: omogeneità
H1: eterogeneità
Accetteremo l’ipotesi nulla di omogeneità se il p-value è >0,05 e quindi useremo un modello a effetti fissi, altrimenti accetteremo l’ipotesi di eterogeneità e useremo un modello a effetti random.
Un ulteriore valore, a conferma del risultato del test, che solitamente si riporta è l’indice I2 che varia tra 0% e 100% e più è alto tanto più è presente eterogeneità nei dati. Una volta scelto il modello possiamo procedere con il problema di Publication bias!
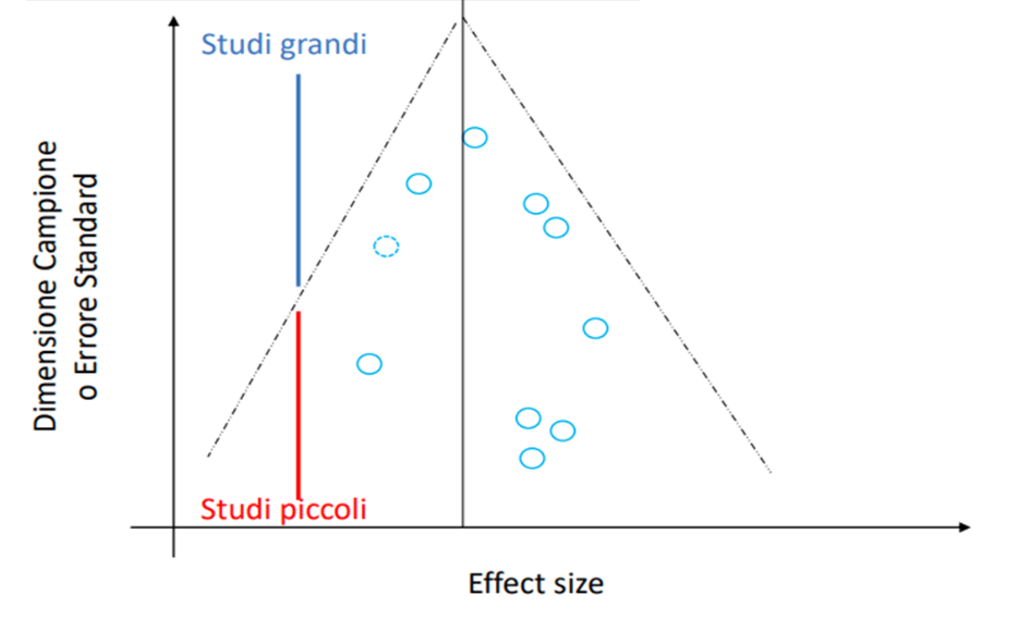
Publication bias: test di Egger
Per verificare se nel nostro caso è presente il problema del Publication Bias, oltre al Funnel Plot (lo vedremo nei paragrafi successivi), possiamo fare il test di Egger:
H0: Publication bias assente
H1: Publication bias presente
Se accettiamo l’ipotesi nulla, ovvero se il p-value è >0,05, allora non abbiamo il problema del Publication Bias, anche se nel funnel plot alcuni studi fossero posizionati all’esterno delle bande del grafico, altrimenti dobbiamo individuare quali studi causano il problema e ripetere l’analisi escludendoli.
Se hai bisogna di una consulenza non esitare a contattarci!
Effetto globale: significativo o no?
Una volta che abbiamo deciso il modello da usare e verificato che non ci siano problemi di Publication bias, possiamo procedere alla lettura dei risultati: vengono riportate diverse misure, tra le quali le più importanti sono l’effect size di ogni singolo studio con il relativo p-value e il peso che ha ciascuno studio nell’analisi.
Per quanto riguarda l’effect size, se questo risulta significativo (p<0,05) vuol dire che l’effetto ottenuto è significativo e più il valore dell’effect size è alto tanto più è elevata la forza dell’effetto che si ha; non tutti gli studi avranno un effetto significativo né un effect size di stesso segno (alcuni avranno effetto positivo e altri negativo). Il peso che uno studio ha nell’analisi, invece, dipende dalla grandezza del campione.
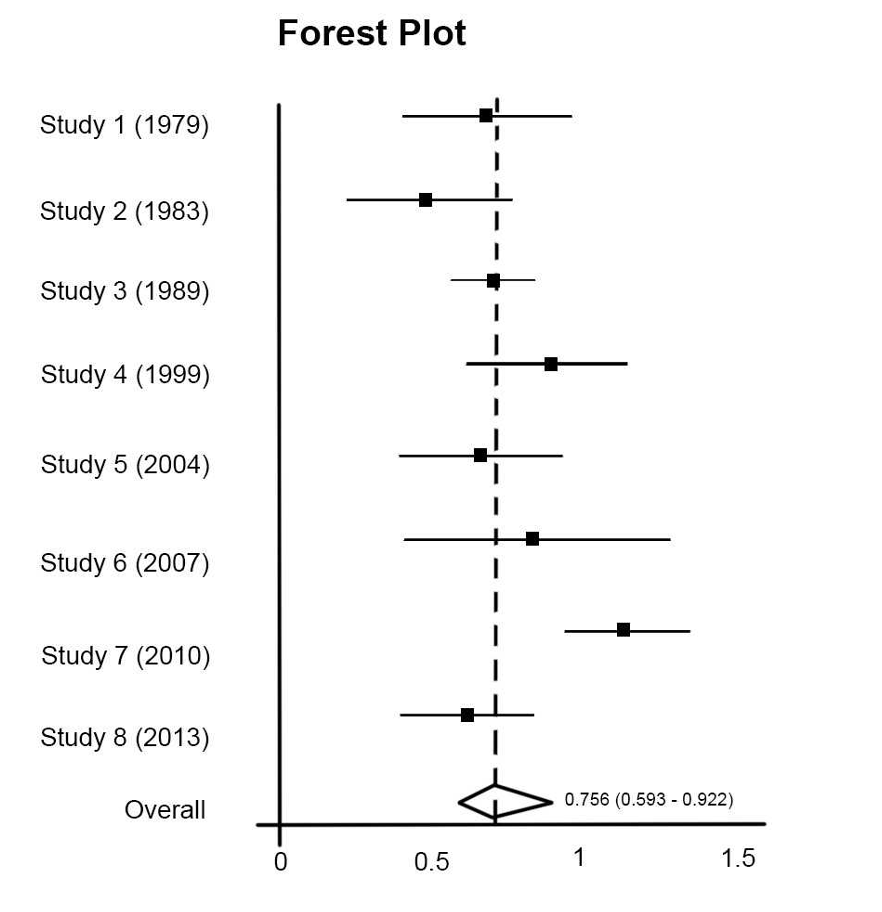
Infine, si ha l’effect size complessivo del fenomeno e il relativo p-value: in base ai valori ottenuti si conclude se l’effetto globale sia significativo e, in tal caso, quale sia la potenza dell’effetto. Per vedere anche visivamente i risultati si riportano il Forest plot e il Funnel plot.
Forest plot
Con questo tipo di grafico si ha un riassunto visivo di ciò che si è osservato numericamente: gli studi (rappresentati dai quadrati) il cui intervallo non comprende l’effetto nullo sono quelli con un effetto significativo; l’intervallo posto più in basso è relativo all’effetto totale (rappresentato da un rombo) e, come per gli effetti dei singoli studi, se non comprende l’effetto nullo allora è significativo.
Vengono, generalmente, riportati anche i pesi, le significatività, l’effetto singolo e totale, gli intervalli di confidenza e gli indicatori relativi all’omogeneità (ovvero I2 e test Q di Cochran).
Funnel plot
Un altro grafico che solitamente si riporta è il Funnel plot, utile per individuare gli studi che potrebbero portare a un Publication bias: se il test di Egger è risultato significativo, si vanno a guardare gli studi che escono al di fuori delle bande di confidenza e, in particolare, quelli che rendono asimmetrico il grafico:
Meta-analisi: leave-one-out
Una tecnica che si utilizza quando gli studi non sono troppo numerosi è ripetere più volte l’analisi escludendo ogni volta uno studio diverso: in questo modo, con la tecnica leave-one-out, si va ad osservare se togliendo uno studio in particolare si ha un decisivo cambiamento sull’effetto globale, ovvero si osserva se uno studio ha un impatto maggiore degli altri nell’analisi.
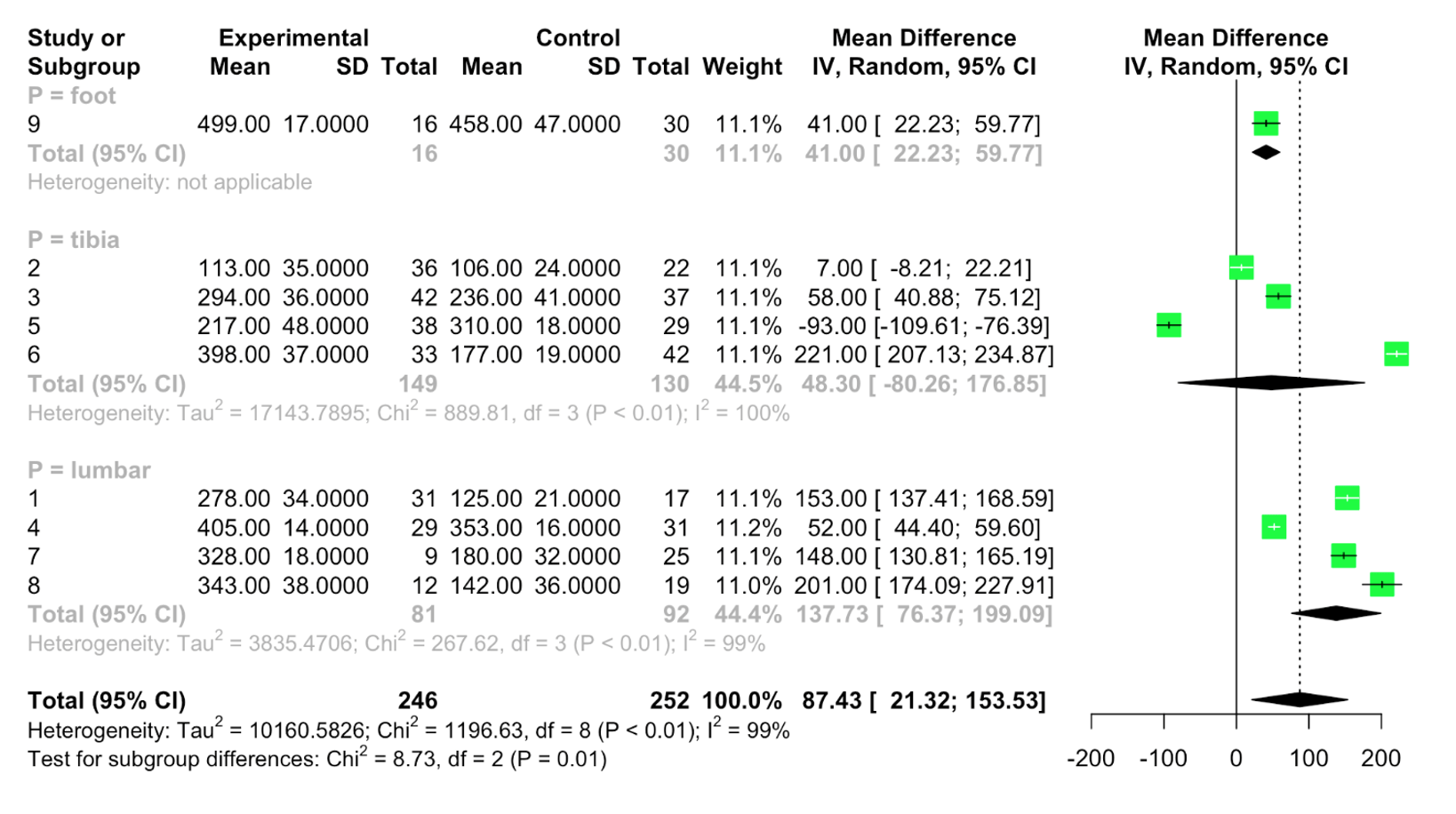
Meta-analisi per sottogruppi
Un’altra tipologia di sotto-analisi che si potrebbe condurre riguarda la suddivisione degli studi in gruppi, ad esempio per tipologia di studio o per paese: in questa maniera si va a osservare se vi sia un effetto particolare in qualche gruppo (consiste nel fare una meta-analisi in cui si ha sotto divisione ulteriore).
Un esempio di Forest plot che si ottiene in questi casi è il seguente:
Meta-analisi: SPSS, R o Stata?
I software con cui possiamo condurre la meta-analisi sono molti: i più comuni sono sicuramente R, Stata e SPSS: R è molto completo e permette di fare molte tipologie diverse di meta-analisi e permette di realizzare dei grafici molto completi, ma bisogna saper programmare; SPSS è molto semplice da usare, ma si possono fare poche tipologie di meta-analisi, però non serve saper scrivere codice; infine Stata è una via di mezzo tra gli altri due software in quanto permette di fare diverse tipologie di meta-analisi sia programmando che usando il menù a tendina!
Per saperne di più leggi gli altri nostri articoli specifici sulle diverse tipologie di meta-analisi!
Sei interessato a imparare i dettagli i 4 ore? Puoi iscriverti a uno dei nostri seminari teorici e pratici sulla meta-analisi con SPSS o con R!

Articolo a cura della Dott.ssa Alessandra Cardinale





