Curva ROC in statistica: che cos’è

La curva ROC, nota anche come Receiving Operating Characteristics, è una tecnica statistica usata in molti ambiti, in particolare in quello medico.
La curva ROC viene utilizzata in presenza di:

Variabili dicotomiche (o binarie), che rappresentino l’esito oggetto di interesse, per esempio un paziente sano oppure malato;
Variabili numeriche (o quantitative), che rappresentino la variabile di un test rispetto alla quale si vuole fare cercare un cut-off (ovvero una soglia) ottimale sopra o sotto il quale assegnare un’unità (per esempio un paziente) a una delle due categorie considerate (per esempio sano e malato).

Vediamo come costruire e interpretare una curva ROC!

A cosa serve una Curva ROC e come si interpreta

La curva ROC è quindi una tecnica statistica standard per riassumere le prestazioni di un classificatore: l’obiettivo, ovviamente, è cercare di ottenere l’errore più piccolo possibile.

Per capire come interpretare la curva ROC andiamo a guardare il seguente esempio in ambito medico, che può in ogni caso essere generalizzato a qualsiasi ambito
Iniziamo definendo i concetti di Vero Positivo (VP), Vero Negativo (VN), Falso Positivo (FP) e Falso Negativo (FN).
Supponiamo di avere 100 pazienti, di cui 60 sani (modalità detta “negativa”) e 40 malati (modalità detta “positiva”) e supponiamo di aver eseguito la classificazione attraverso un qualche modello, dal quale abbiamo ottenuto 50 pazienti sani e 50 malati. Costruendo la tabella doppia otteniamo il seguente risultato:

Sulla diagonale abbiamo i pazienti classificati correttamente, ovvero 30 soggetti sono malati e sono classificati come tali e 40 soggetti sono sani e sono stati classificati come tali. Gli altri valori, invece, sono i pazienti classificati in modo errato: 10 pazienti, la cui categoria reale è “malati” sono stati previsti come “sani”, viceversa 20 pazienti la cui categoria reale è “sani” sono stati previsti come “malati”.
Generalizzando il problema quello che abbiamo è:

dove VP indica i veri positivi, cioè coloro che sono malati e sono stati previsti come tali, allo stesso modo VN indica i veri negativi, FN indica i falsi negativi, cioè coloro che sono malati ma sono stati previsti come sani, allo stesso modo FP indica i falsi positivi.

L’obiettivo è avere un modello che renda FN e FP quanto più vicini possibile a zero: la curva ROC mi aiuta ad ottenere questo obiettivo, infatti – tra tutti i possibili cut-off – mi permette di determinare il cut-off tale da minimizzare FP ed FN.

Per stabilire quanto la previsione fatta sia buona si utilizza un indice chiamato Accuratezza, ovvero il tasso di corretta classificazione, e viene calcolato come:

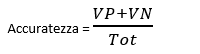
Essendo una proporzione, i suoi valori variano tra 0 e 1 e sarà tanto migliore tanto più si avvicina al valore 1.

Tuttavia, questo indice non è sufficiente per valutare una previsione: supponiamo di avere 90 pazienti sani e 10 malati e di prevederli tutti come sani

Utilizzando la formula dell’accuratezza si ottiene che il tasso di corretta classificazione è pari a (90+0)/100=0.9, ovvero di aver previsto bene 90 pazienti su 100. Il risultato, però, è inutile, in quanto prevede solo pazienti sani, non individuando quelli malati.

Oltre all’accuratezza, quindi, utilizziamo anche altri due indici che ci serviranno per individuare il cut-off ottimale e costruire la curva ROC: la sensibilità e la specificità. Vediamo insieme come calcolarli e perché sono importanti!

Sensibilità, Specificità e Cut-off ottimale

La sensibilità e la specificità sono due ulteriori indici per valutare la possibile classificazione delle unità nei due gruppi di interesse.

La sensibilità fornisce il tasso di corretta classificazione per la categoria dei positivi, cioè coloro che sono stati previsti come positivi sul totale dei positivi (nel nostro esempio dei malati) e si calcola come il rapporto tra VP e P:

Per quanto riguarda la specificità il discorso è analogo, ma è riferito ai negativi (nel nostro esempio ai sani):

Così come per l’accuratezza, anche questi due indici variano tra 0 e 1 e devono essere massimizzati scegliendo il cut-off ottimale, ovvero il valore soglia oltre il quale conviene prevedere esito positivo.

A questo punto la curva ROC viene costruita considerando tutti i possibili valori di cut-off del test (ovvero della variabile numerica) e, per ognuno di essi, si calcolano la sensibilità e la proporzione di falsi positivi, cioè 1-specificità. Congiungendo i punti che mettono in rapporto Sensibilità ed 1-Specificità si ottiene una curva chiamata curva ROC e avrà il seguente aspetto

E ora? Scopriamo nel prossimo paragrafo cosa rappresenta l’area della curva.

Indice AUC nella Curva ROC

Il punto ideale della curva ROC è quello di coordinate (x,y) = (0,1), che rappresenta il caso in cui tutte le osservazioni positive sono classificate correttamente e nessun caso negativo è classificato erroneamente come positivo. Un modello perfetto dal punto di vista discriminatorio è rappresentato, perciò, da una curva ROC che passa per l’angolo superiore sinistro degli assi: l’area della curva è pari a 1.

Al contrario, la curva ROC per un test assolutamente privo di valore informativo è rappresentata dalla retta bisettrice y=x, detta anche “chance line” e l’area della curva è pari a 0.5.

Questi sono, però, i due casi estremi.

In linea generale si ottiene una curva ROC la cui area è compresa tra 0.5 e 1: l’area tra la bisettrice e la curva ROC si chiama AUC (acronimo dei termini inglesi “Area Under the Curve”) ed è un buon indicatore della performance del classificatore al variare della soglia di attribuzione.

Tanto maggiore è l’area sotto la curva (cioè tanto più la curva si avvicina al vertice in alto a sinistra del grafico) tanto maggiore è la capacità della variabile test di discriminare correttamente i due gruppi.

Per l’interpretazione dei valori dell’area sottostante la curva ROC è possibile riferirsi alla classificazione proposta da Swets:

1) AUC=0.5 il test non è informativo;

2) 0.5<AUC≤0.7 il test è poco accurato;

3) 0.7<AUC≤0.9 il test è moderatamente accurato;

4) 0.9<AUC<1.0 il test è altamente accurato;

5) AUC=1 test perfetto.

Come detto, attraverso la curva ROC è possibile identificare il best cut-off, cioè il valore del test che massimizza la somma di Sensibilità e Specificità (ovvero che massimizza la differenza tra Sensibilità e 1-Specificità). Tale differenza è detta Indice di Youden. Sarà dunque sufficiente cercare il valore che massimizza l’indice (tra l’altro questo cut-off coincide con il punto ‘graficamente’ più vicino all’angolo in alto a sinistra della curva ROC).

Nota bene: se Specificità e Sensibilità risultano essere particolarmente squilibrate è possibile scegliere anche un diverso cut-off, anche se non massimizza lo Youden’s Index.

Confronto di diverse Curve ROC

Quando abbiamo più modelli a disposizioni per classificare le osservazioni possiamo confrontare le curve ROC ottenute per capire quale tra i modelli risulti essere il migliore.

Il confronto si baserà sulle aree ottenute, cioè sulle AUC dei modelli: ovviamente il modello che sceglieremo sarà quello cui corrisponde l’area più grande (nella figura sottostante corrisponde alla curva blu).

Curva ROC: meglio in SPSS, R o Excel?

Come calcolare la curva ROC? Per quanto riguarda Excel, il suo uso in ambito statistico è generalmente sconsigliato. Per quanto riguarda le Curve ROC useremo Excel come appoggio per l’analisi condotta su SPSS.

Su SPSS il calcolo dello Youden’s Index va fatto manualmente poiché il software non lo fornisce in automatico.

Sul menù Analizza clicchiamo su Curva ROC:

Quello che SPSS restituisce è il grafico della curva ROC, il test d’ipotesi che va a verificare l’ipotesi nulla di AUC = 0,5, ovvero di variabile test non informativa (cioè per nulla in grado di discriminare) e una tabella in cui vengono riportati tre colonne: i cut-off possibili e i corrispondenti valori di sensibilità e di 1-specificità.

A questo punto basta copiare la tabella su Excel e creare la colonna dello Youden Index andando a sottrarre a ogni valore della sensibilità quello di 1-specificità: si va a guardare il valore più grande dello Youden Index e il corrisponde cut-off sarà quello ottimale.

Nell’esempio sottostante risulta che il valore più grande dello Youden Index è 0.59, a cui corrispondono un cut-off pari a 83, una sensibilità pari a circa 0.71 e una specificità pari a 1-0.118=0.882.

Per quanto riguarda il software R, invece, esistono molti pacchetti che possiamo utilizzare. Qui vediamo l’uso del pacchetto pROC.

Dopo aver importato i dati, carichiamo la libreria pROC e eseguiamo i seguenti comandi:

response indica la variabile categorica binaria;
predictor indica la variabile scala di interesse;
auc è il parametro che indica se vogliamo calcolare l’area sotto la curva ROC;
plot è un parametro che indica se vogliamo il disegno della curva ROC;
col indica il colore della curva;
identity è il parametro che indica se vogliamo la retta bisettrice nel grafico della curva ROC;
identity.col indica il colore della bisettrice nel grafico della curva ROC;
identity.lty indica il tipo tratteggio della bisettrice nel grafico della curva ROC;
legacy.axes è il parametro che indica se vogliamo l’asse delle x orientato nel verso corretto;
main è il titolo che vogliamo dare al grafico della curva ROC;
xlab e y lab sono i nomi che vogliamo dare agli assi cartesiani nel grafico della curva ROC;
print.auc è il parametro che indica se vogliamo che compaia l’etichetta contenente il valore dell’area AUC.

Successivamente se vogliamo calcolare lo Youden Index e quindi il cut-off ottimale dobbiamo creare un dataset contenente la colonna delle soglie, la colonna delle sensibilità e la colonna di 1-specificità; successivamente calcoliamo il vettore dello Youden Index andando a sottrarre a ogni valore della sensibilità quello di 1-specificità e aggiungiamo questa nuova colonna al dataset: si va a guardare il valore più grande dello Youden Index e il corrisponde cut-off sarà quello ottimale.

Come nell’esempio precedente risulta che il valore più grande dello Youden Index è 0.59, a cui corrispondono un cut-off pari a 83, una sensibilità pari a circa 0.71 e una specificità pari a 1-0.118=0.882:

Se hai ancora dei dubbi e vuoi una consulenza su questo argomento, così come su tanti altri, oppure vuoi affidarci la tua lavoro di analisi non esitare a contattarci!

Se sei interessato ad imparare ad utilizzare SPSS per fare analisi di statistica medica, troverai in questa pagina i dettagli del Corso Online di Fondamenti di Statistica medica in SPSS che dura 16 ore ed eroghiamo comodamente online.

Articolo a cura della Dott.ssa Alessandra Cardinale